ความคลาดเคลื่อนเชิงตำแหน่งในภาพถ่าย

จาก ChulaPedia

---

รุ่นปัจจุบันของ 09:02, 21 มีนาคม 2554

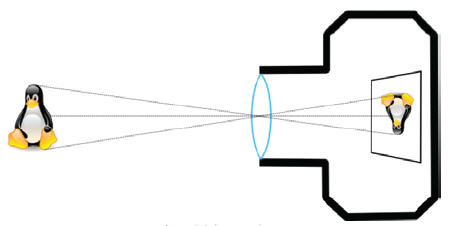
เมื่อพิจารณาภาพถ่ายในช่วงคลื่นแสงที่ได้จากกล้องถ่ายภาพ โดยเฉพาะภาพถ่ายภูมิประเทศเช่นที่เห็นในภาพที่ 1 จะสามารถรู้สึกได้ถึงความผิดปกติทางตำแหน่งหรือขนาดของวัตถุที่ปรากฏในภาพถ่าย ดังจะเห็นได้จากภาพที่ 1 ว่าที่ระยะไกลออกไป ภาพของรางรถไฟดูเหมือนจะแคบลงจนลู่เข้าหากัน แต่ข้อเท็จจริงที่เราทราบกันดีก็คือรางรถไฟทั้งสองข้างจะขนานกัน ลักษณะดังกล่าวไม่ได้เกิดจากความผิดพลาดของกล้องถ่ายภาพแต่เป็นธรรมชาติที่เกิดขึ้นตามปกติของการถ่ายภาพอันเป็นปรากฏการณ์ที่แสงจากวัตถุเดินทางผ่านเลนส์ไปเกิดภาพในกล้องถ่ายภาพ ดังแสดงในภาพที่ 2 ในทางทฤษฏีสามารถอธิบายปรากฏการณ์นี้ว่าเป็นลักษณะเรขาคณิตแบบการฉายผ่านจุดศูนย์กลางการฉาย (perspective projection) ซึ่งส่งผลให้ภาพของวัตถุที่ปรากฏในภาพถ่ายมีมาตราส่วนไม่คงที่ขึ้นอยู่กับระยะจากวัตถุถึงกล้องถ่ายภาพ ดังจะเห็นได้จากภาพที่ 1 ว่าส่วนของรางรถไฟที่อยู่ใกล้กับกล้องถ่ายภาพจะปรากฏว่ามีขนาดใหญ่กว่าส่วนของรางที่อยู่ไกลออกไป (ทำให้เห็นว่ารางรถไฟค่อยๆ ลู่เข้าหากัน) นอกเหนือจากลักษณะเรขาคณิตดังกล่าวแล้วก็ยังมีปัจจัยอื่นที่ส่งผลต่อตำแหน่งของวัตถุในภาพถ่ายอีก ทั้งที่มาจากธรรมชาติของการถ่ายภาพและที่มาจากความคลาดเคลื่อนในเครื่องมือรวมทั้งกระบวนการในการถ่ายภาพและผลิตภาพถ่าย

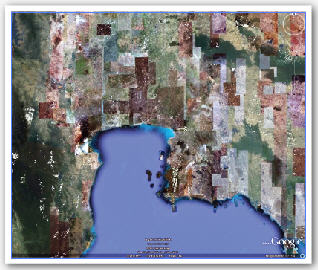
การที่จะนำภาพถ่ายมารังวัดเพื่อให้ทราบค่าพิกัดของวัตถุในภูมิประเทศที่มีความละเอียดถูกต้องตามต้องการนั้นจำเป็นต้องมีวิธีขจัดความคลาดเคลื่อนเชิงตำแหน่งออกไป โดยทั่วไปสามารถกระทำได้ 2 แนวทาง แนวทางแรกเป็นการรังวัดค่าพิกัดของวัตถุจากภาพถ่ายเดิมแล้วนำค่าพิกัดที่ได้ไปคำนวณในสมการที่เหมาะสมเพื่อให้ได้ค่าพิกัดของวัตถุในภูมิประเทศที่มีความละเอียดถูกต้องตามต้องการ แนวทางนี้ไม่ค่อยจะเหมาะสมกับผู้ใช้ภาพถ่ายที่ไม่มีความรู้ทางทฤษฏีเกี่ยวกับลักษณะเรขาคณิตเท่าใดนักเนื่องจากมีความยุ่งยากซับซ้อนในการคำนวณค่าพิกัด ส่วนแนวทางที่สองจะเป็นการนำภาพถ่ายเดิมไปผ่านกระบวนการดัดแก้ภาพถ่าย (image rectification) ให้ได้เป็นภาพถ่ายที่ดัดแก้แล้วซึ่งค่าพิกัดของวัตถุในภาพถ่ายจะสอดคล้องกับค่าพิกัดในภูมิประเทศ (ตามมาตราส่วน) ความยุ่งยากซับซ้อนจะอยู่ในกระบวนการดัดแก้ภาพถ่ายซึ่งจะต้องมีการใช้สมการที่เหมาะสมในการคำนวณคล้ายกับในแนวทางแรก แต่สำหรับผู้ที่นำภาพถ่ายที่ดัดแก้แล้วไปใช้งานก็จะได้รับความสะดวกโดยที่สามารถรังวัดค่าพิกัดบนภาพถ่ายแล้วแปลงเป็นให้ค่าพิกัดในภูมิประเทศได้เพียวแค่คำนวณตามมาตราส่วนเท่านั้น ตัวอย่างหนึ่งของภาพถ่ายที่ได้รับการดัดแก้แล้วที่ถูกนำไปใช้งานอย่างแพร่หลายมากก็คือ ภาพถ่ายพื้นผิวโลกที่มีอยู่ใน Google Earth (ดังในภาพที่ 3) ซึ่งประกอบด้วยภาพถ่ายจำนวนมากมาต่อกัน

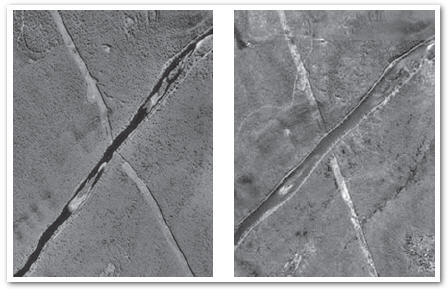
การดัดแก้ภาพถ่ายสามารถกระทำได้หลายวิธี ตั้งแต่การดัดแก้ที่ไม่ต้องการความถูกต้องสูงที่ใช้สมการอย่างง่ายและข้อมูลเพิ่มเติมไม่มากนักไปจนถึงการดัดแก้ที่ให้ความละเอียดถูกต้องสูง ใช้สมการที่ซับซ้อน รวมทั้งต้องใช้ข้อมูลเพิ่มเติมอีกมาก การดัดแก้ภาพถ่ายที่ให้ความละเอียดถูกต้องสูงที่นิยมใช้กันในปัจจุบันคือ การดัดแก้ออร์โธ (orthorectification) ภาพที่ได้จากวิธีการนี้เรียกว่า ภาพออร์โธ (orthophoto หรือ orthoimage) ภาพที่ 4 แสดงให้เห็นความแตกต่างระหว่างภาพถ่ายธรรมดากับภาพถ่ายที่ได้รับการดัดแก้เป็นภาพออร์โธ แนวเส้นตรงที่พาดผ่านภูมิประเทศที่มีความสูงต่ำแตกต่างกันปรากฏเป็นแนวที่คดงอในภาพถ่ายด้านซ้าย แต่เมื่อภาพถ่ายได้รับการดัดแก้จนได้เป็นภาพออร์โธแล้วแนวดังกล่าวก็จะปรากฏเป็นเส้นตรง

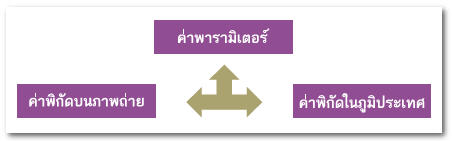
สมการที่นิยมนำมาใช้สำหรับการคำนวณในการขจัดความคลาดเคลื่อนเชิงตำแหน่งนั้น มีชื่อเรียกทางทฤษฏี (ที่ไม่ค่อยตรงกับความหมายนัก) ว่า แบบจำลองอุปกรณ์รับรู้ (sensor model) เป็นสมการที่แสดงถึงความสัมพันธ์ขององค์ประกอบต่างๆ ของการถ่ายภาพซึ่งสามารแบ่งออกเป็นกลุ่มๆ ได้ 3 กลุ่มคือ ค่าพิกัดของจุดบนภาพถ่าย ค่าพิกัดของจุดๆ นั้นในภูมิประเทศ และค่าพารามิเตอร์ของภาพถ่าย ดังในภาพที่ 5 จากความสัมพันธ์ในภาพที่ 5 สามารถอธิบายอย่างง่ายๆ ได้ว่า ถ้าเราทราบค่าองค์ประกอบ 2 กลุ่ม ก็จะสามารถคำนวณหาค่าองค์ประกอบอีกกลุ่มหนึ่งที่ไม่ทราบค่าได้ ดังนั้นในแนวทางแรกของการขจัดความคลาดเคลื่อนเชิงตำแหน่ง ถ้าทราบค่าพารามิเตอร์ของภาพถ่ายและวัดค่าพิกัดของวัตถุบนภาพถ่ายที่สนใจมาได้ เราก็จะสามารถคำนวณหาค่าพิกัดของวัตถุนั้นในภูมิประเทศได้โดยอาศัยแบบจำลองอุปกรณ์รับรู้ (ในกรณีที่ต้องการค่าพิกัด 3 มิติต้องใช้ภาพถ่าย 2 ภาพ) สำหรับในแนวทางที่ 2 ซึ่งเป็นการดัดแก้ภาพถ่ายก็จะสามารถใช้แบบจำลองอุปกรณ์รับรู้ในการคำนวณเช่นกัน แต่จะเป็นการคำนวณในทางกลับกัน คือ ถ้าทราบค่าพารามิเตอร์ของภาพถ่าย แล้วกำหนดค่าพิกัดของจุดในภูมิประเทศ เราก็จะใช้แบบจำลองอุปกรณ์รับรู้ในการคำนวณว่าจุดๆ นั้นมีค่าพิกัดเท่าใดบนภาพถ่าย

ความก้าวหน้าทางเทคโนโลยีในปัจจุบันทำให้การผลิตภาพถ่ายทางพื้นดิน ทางอากาศ และจากดาวเทียมสามารถกระทำได้อย่างสะดวก รวดเร็ว และเสียค่าใช้จ่ายไม่มากนักเมื่อเทียบกับในอดีต คนทั่วไปสามารถเข้าถึงข้อมูลเหล่านี้ได้ง่ายโดยเฉพาะอย่างยิ่งการเข้าถึงผ่านช่องทางของอินเทอร์เน็ต การมีความรู้ความเข้าใจในธรรมชาติของภาพถ่ายเกี่ยวกับเรื่องความคลาดเคลื่อนเชิงตำแหน่งและการขจัดความคลาดเคลื่อนดังกล่าวจะช่วยให้เราสามารถนำภาพถ่ายไปใช้งานให้เกิดประโยชน์ได้มากยิ่งขึ้น

อาจารย์ผู้ดูแลบทความ พ.อ. ดร.กนก วีรวงศ์ อาจารย์ประจำภาควิชาวิศวกรรมสำรวจ

ผู้รับผิดชอบบทความ ศูนย์การสื่อสารนานาชาติแห่งจุฬาฯ